カオスな世界
ロジスティック写像
x(t+1) = a * x(t) * (1- x(t)) を考えます.この式は,生物の数の増減を表すモデルとして用いられ,ロジスティック写像と呼ばれています.
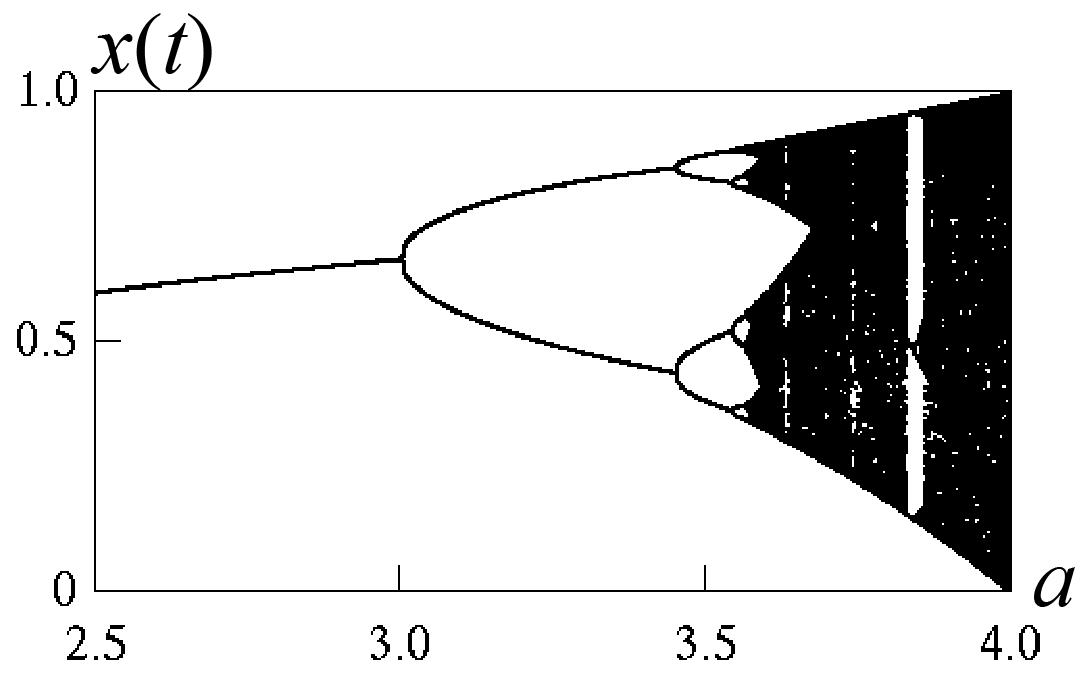
ここで t は 0, 1, 2, …の値をとります.x(0) と a を決めると x(1) (= a * x(0) * (1 - x(0)) が求まります.これを繰り返すと x(1), x(2), … が順次求まります.a の値を変えていった場合の x(10000) ~x(11000)の値を左の図に示します.
a が3ぐらいまでは x(10000)~x(11000) が1点になっていることがわかります.a が3辺りで1点になっていた x が2点になっています.それが4点,8点,16点と倍になっていき a = 4 では x(10000)~ x(11000) は 0から1の間を埋め尽くしています.
このような状態をカオスといいます.
カオスの応用(短期予測)
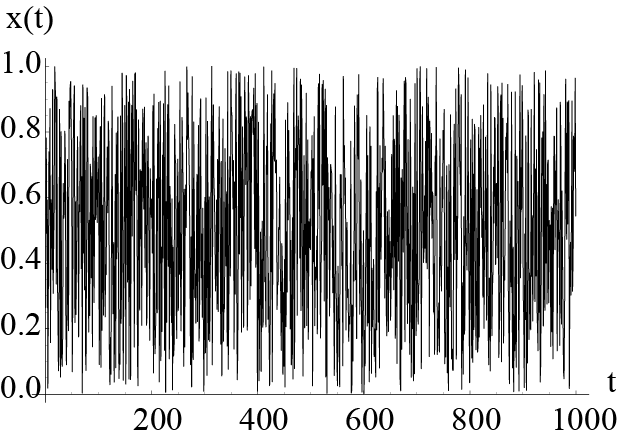
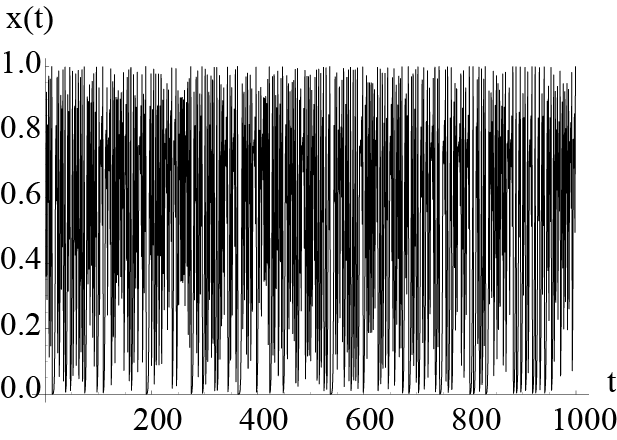
2つの波形を見てください.
横軸は時刻tで縦軸は何かの観測値(x(t), 例えば毎日の株価の値,ある地点での温度,インフルエンザの患者数などです.最大値が1に,最小値が0になるように操作しています)
2つの波形を見ただけでは違いはわかりません.
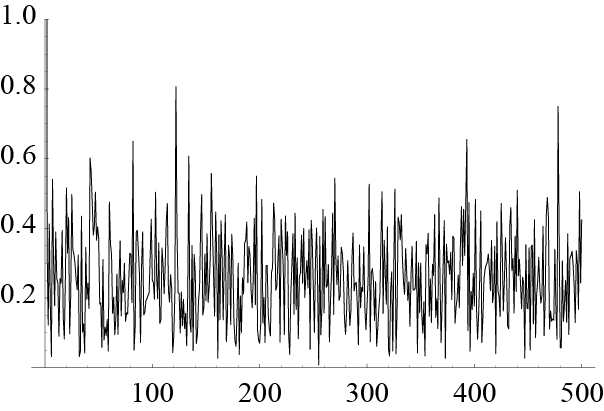
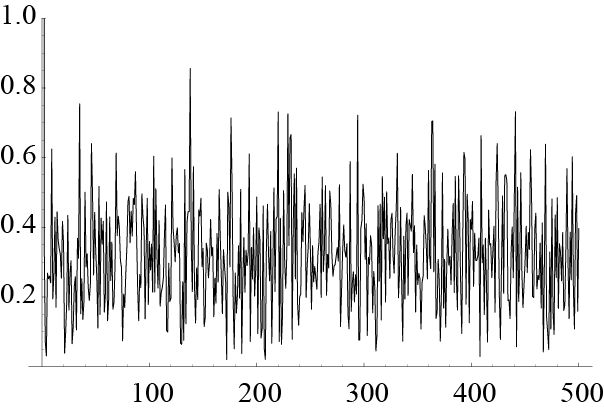
時間波形では違いが分からない場合は,フーリエ変換(注1)というのを行い周波数成分をみます.
周波数成分を見ても違いがわかりません??
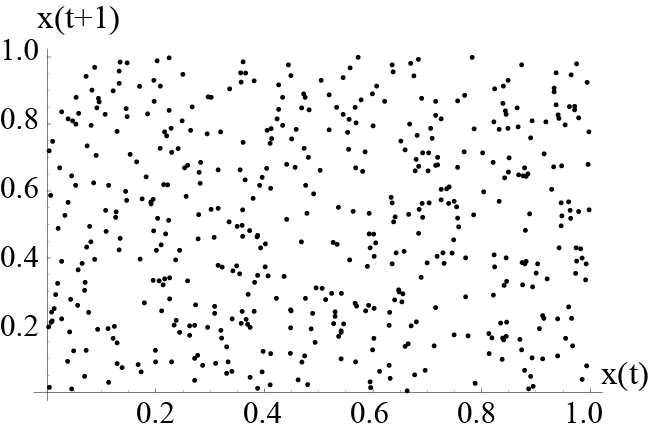
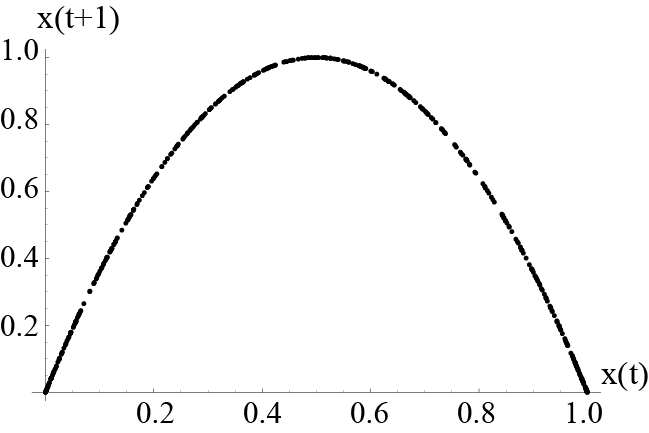
次に埋め込みという作業を行ってみます.時間波形のデータから連続する2点(x(t)とx(t+1)とする)をとってきて2次元平面の点としてプロットします.全てのデータに対してその作業を行うと,時間波形1のデータは左図へ,時間波形2のデータは右図へと変換されます.
波形1埋め込みの図からは今の状態から次の状態( x(t) から x(t+1)) への変化ルールが見えませんが,波形2の埋め込み(右図)からはルールが分かります.すなわち,こちらは今の状態 (x(t)) がわかれば次の状態 (x(t+1)) が分かることを意味します.
例えば,株価の毎日の変動データを取ってきて「埋め込み2」のような構造が分かれば,今日の株価 (x(t)) から明日の株価 (x(t+1)) が正確に予測できることを意味します.
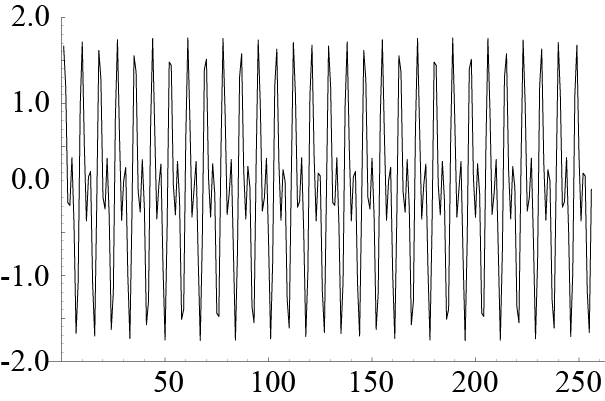
横軸は時刻.
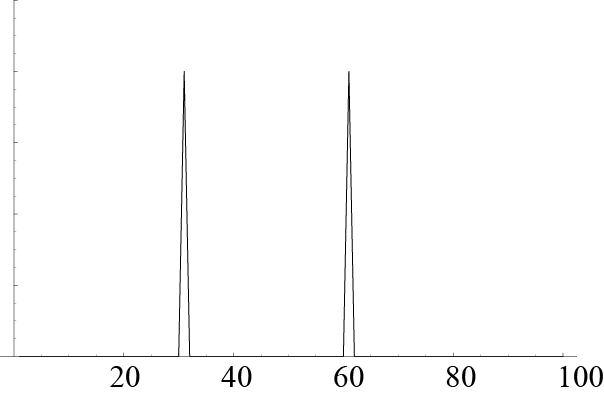
横軸は周波数.
フーリエ変換とは?
左図の時間波形(sin(2π*30*t)+sin(2π*60*t)をグラフ表示している.)があるときに,フーリエ変換すると右図の周波数成分の図が得られる.
元の式(sin(2π*30*t)+sin(2π*60*t))の周波数に対応する30と60にピークが現れている.
従って,式が分からなくても時間波形データより,周波数30と60の合成波であることがフーリエ変換よりわかる.