●例
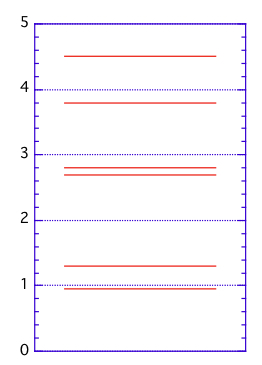を 
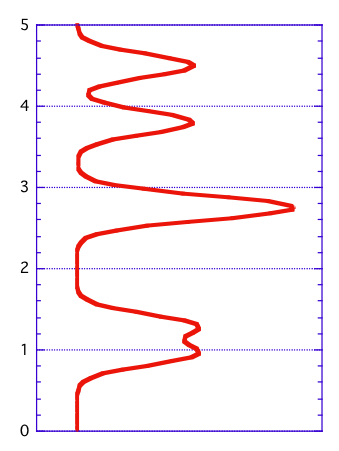に変換する。
●ガウス関数の基礎
令和5年6月30日 更新
●例
を に変換する。
●ガウス関数の基礎
例えば、ある学校（生徒数750人）のテストの成績が、次のような
グラフで表されるとします（横軸は得点、縦軸はその人数。満点が100点で平均点が50点）。
このとき、x = 0からx = 100の範囲でこのグラフで囲まれた部分の面積が
750となります。
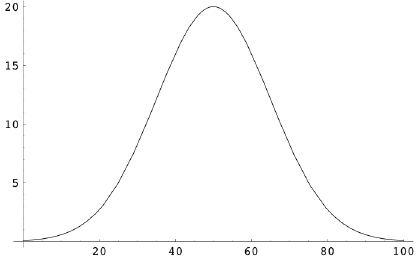
一般に、自然界で起こるあらゆる現象は、このような曲線で表されると
言われています。この曲線を正規分布、またはガウス関数と呼んでいます。
ガウス関数の一般式は、次のようになっています。
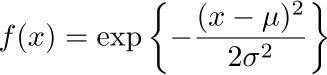
このグラフで囲まれた面積を1とするために、通常は、次の式のように
規格化します。
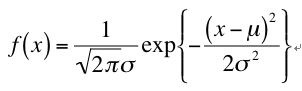（式1）
ここでμは平均、σは標準偏差（σ2は分散）を表します。μをゼロとすると
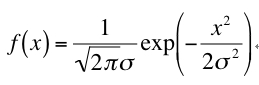（式2）
となり、y軸に対して左右対称の関数になります。
図1にσ = 1およびσ = 2の場合を図示します。
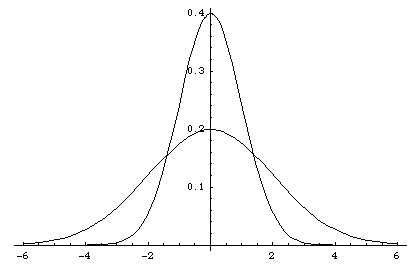
図1：ガウス関数（式2）。
σ = 1（細長い方）、σ = 2（幅広い方）。
x軸と囲まれた面積は、σの値によらず1となります。
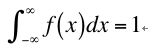（式3）
●ガウス関数の数学的な特徴
（変曲点）
x = ±σで変曲点をとります。
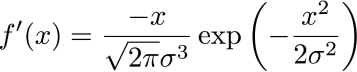
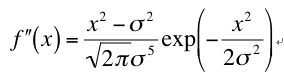（式4）
（最大値）
x = 0で最大値hをとります。
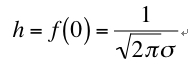（式5）
ちなみに
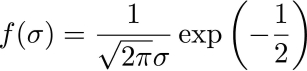
なので，変曲点における高さは，最大値の約0.6倍です。
（半値幅）
のとき、最大値の半分の高さ
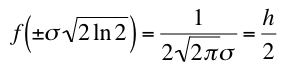（式6）
になります。このときのx座標の左右の広がりの幅
を半値幅(FWHM)と呼びます。
実験などで半値幅が求められるならば
（式7）
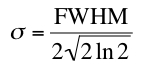（式8）
によって標準偏差を求めることが出来ます。
なので，半値幅を2.4で割れば標準偏差σが得られます。
●ガウス分布の確率
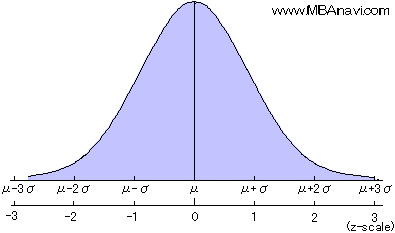
（図は，こちらから引用しました）
ガウス分布は確率を表します。
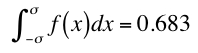（式9）
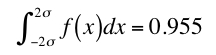（式10）
|
-σからσまでの範囲
|
68.3％
|
|
-2σから2σまでの範囲
|
95.5％
|
|
-3σから3σまでの範囲
|
99.7％
|
だからCrystalStructureでは3σの範囲で十分です。
●EXCEL関数normsdistを用いるときの注意
|
Z
|
=normsdist(Z)
|
意味
|
確率
|
|
0
|
0.500
|
0.5+0.000
|
0.00％
|
|
1
|
0.841
|
0.5+0.341
|
68.3％
|
|
2
|
0.977
|
0.5+0.477
|
95.5％
|
|
3
|
0.999
|
0.5+0.499
|
99.7％
|
関数normsdistをそのまま使ってしまうと
確率の値が大きくなってしまいます。
これは、半分（0.5）から始まるためです。
累積値であることに注意してください。
具体的には、0.5を引いて二倍すれば確率になります。
●EXCELを用いるときの便利な関数例
|
平均
|
=average(範囲)
|
|
正規分布
|
=normdist(x,μ,σ,false)
|
|
標準正規累積分布
|
=normsdist(Z)
|
|
標準偏差（s）；標本
|
=stdev(範囲)
|
|
標準偏差（σ）；母集団
|
=stdevp(範囲)
|
EXCELで書くときの具体例
|
A
|
B
|
C
|
D
|
E
|
|
|
1
|
幅
|
10
|
|||
|
2
|
x
|
250
|
387
|
399
|
412
|
|
3
|
100
|
=normdist($A3,B$2,$B$1,false)
|
|
|
|
|
4
|
101
|
|
|
|
|
|
5
|
102
|
|
|
|
|
|
6
|
103
|
|
|
|
|
後は、B3セルを縦横にコピーする。最後に合計(total)を忘れないように。
$A3；xは必ずA列目だから絶対座標$Aとする。
B$2；μは必ず2行目だから絶対座標$2とする。
$B$1；σは必ずB1だから絶対座標$B$1とする。
false；もしもtrueにすると関数は累積になる。
このページ作成のメモ
母集団の平均は、標本から得られた平均の分布の平均に一致する。
母集団の標準偏差は、標本から得られた平均の分布の標準偏差よりも大きい。
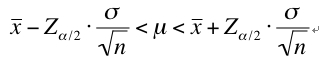
香川大学工学部材料創造工学科 石井知彦